Isogeometric finite elements for shells

Abstract

Hierarchische Balken-, Platten- und Schalenformulierungen basieren auf einer geschickten Reparametrisierung der kinematischen Gleichungen, die sich für neuartige, glatte Diskretisierungsverfahren als vorteilhaft erweist. Im vorliegenden Beitrag werden die intrinsischen Eigenschaften des hierarchischen Konzepts anhand statischer und dynamischer Analysen von Flächentragwerken aufgezeigt und diskutiert.

Abstract

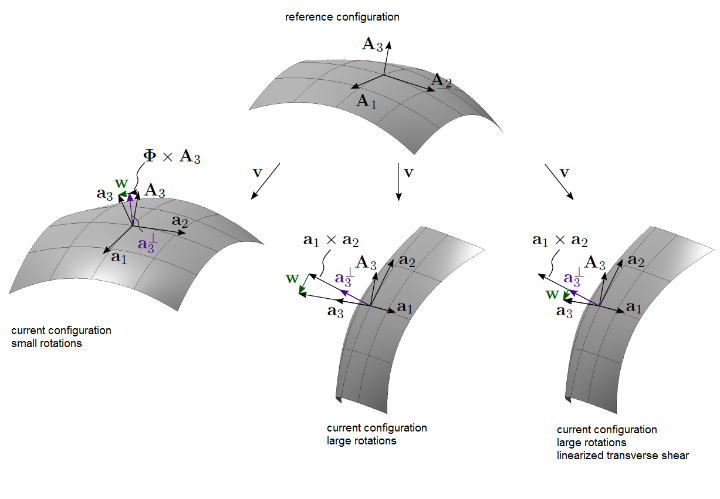
Consistent treatment of large rotations in common Reissner–Mindlin formula-tions is a complicated task. Reissner–Mindlin formulations that use a hierarchicparametrization provide an elegant way to facilitate large rotation shell anal-yses. This can be achieved by the assumption of linearized transverse shearstrains, resulting in an additive split of strain components, which technicallysimplifies implementation of corresponding shell finite elements. The presentstudy aims at validating this assumption by systematically comparing numeri-cal solutions with those of a newly implemented hierarchic and fully nonlinearReissner–Mindlin shell element.

Abstract

We present a comprehensive study on the approximation power of NURBS and the significance of exact geometry in stability analyses of shells. Pre-buckling analyses are carried out to estimate the critical load levels and the initial buckling patterns. Various finite element solutions obtained with the commercial code ANSYS are compared with solutions from the isogeometric version of the finite element method, using our in-house code NumPro. In some problem setups, the isogeometric shell elements provide superior accuracy compared to standard (as opposed to isogeometric) shell finite elements, requiring only a fractional amount of degrees of freedom for the same level of accuracy. The present study systematically investigates the sources of this superior accuracy of the isogeometric approach. In particular, hypotheses are tested concerning the influence of exact geometry and smoothness of splines.

Abstract

In all structural models, the section or fiber response is a relation between the strain measures and the stress resultants. This relation can only be expressed in a simple analytical form when the material response is linear elastic. For other, more complex and interesting situations, kinematic and kinetic hypotheses need to be invoked, and a constrained three-dimensional constitutive relation has to be employed at every point of the section in order to implement non-linear and dissipative constitutive laws into dimensionally reduced structural models. In this article we explain in which sense reduced constitutive models can be expressed as minimization problems, helping to formulate the global equilibrium as a single optimization problem. Casting the problem this way has implications from the mathematical and numerical points of view, naturally defining error indicators. General purpose solution algorithms for constrained material response, with and without optimization character, are discussed and provided in an open-source library.

Abstract

We develop a mixed geometrically nonlinear isogeometric Reissner–Mindlin shell element for the analysis of thin-walled structures that leverages Bézier dual basis functions to address both shear and membrane locking and to improve the quality of computed stresses. The accuracy of computed solutions over coarse meshes, that have highly non-interpolatory control meshes, is achieved through the application of a continuous rotational approach. The starting point of the formulation is the modified Hellinger–Reissner variational principle with independent displacement, membrane, and shear strains as the unknown fields. To overcome locking, the strain variables are interpolated with lower-order spline bases while the variations of the strain variables are interpolated with the corresponding Bézier dual bases. Leveraging the orthogonality property of the Bézier dual basis, the strain variables are condensed out of the system with only a slight increase in the bandwidth of the resulting linear system. The condensed approach preserves the accuracy of the non-condensed mixed approach but with fewer degrees of freedom. From a practical point of view, since the Bézier dual basis is completely specified through Bézier extraction, any spline space that admits Bézier extraction can utilize the proposed approach directly.

Abstract

We present a variational method for problems in solid and structural mechanics that is designed to be intrinsically free from locking when using equal order interpolation for all involved fields. The specific feature of the formulation is that it avoids all geometrical locking effects (as opposed to material locking effects, e.g. Poisson locking) for any type of structural or solid model, independent of the underlying discretization scheme. The possibility to employ equal order interpolation for all involved fields circumvents the task of finding particular function spaces to remove locking and avoid artificial stress oscillations. This is particularly attractive for instance for isogeometric analysis using unstructured meshes or T-splines. Comprehensive numerical tests underline the promising behaviour of the proposed method for geometrically linear and non-linear problems in terms of displacements and stress resultants using standard finite elements, isogeometric finite elements and a meshless method.

Abstract

Angesichts einer stetig steigenden Anzahl komplexer Diskretisierungsverfahren beschäftigt sich die vorliegende Arbeit mit intrinsisch lockingfreien Schalenformulierungen. Aus der Literatur bekannte Konzepte versuchen stets die durch die Diskretisierung entstehenden Locking-Effekte zu beseitigen oder abzumindern. Tritt Locking jedoch gar nicht auf, ist dessen Beseitigung obsolet. Deshalb sollen die hier vorgestellten Schalenformulierungen numerische Locking-Effekte bereits auf Theorieebene vermeiden, ungeachtet vom verwendeten Diskretisierungsschema. Die Vermeidung von Locking bereits vor der Diskretisierung verspricht ein breites Anwendungsspektrum für diverse Diskretisierungsverfahren im Bereich von Computersimulationen physikalischer Vorgänge. Der erste Teil dieser Arbeit beschäftigt sich mit der intrinsischen Vermeidung von Querschublocking in Formulierungen für Strukturtheorien. Über hierarchische Reparametrisierung der kinematischen Gleichungen kann Querschublocking im Rahmen einer primalen Methode a priori vermieden werden. Das Konzept wird gleichermaßen für schubweiche Balken-, Platten- und Schalenformulierungen demonstriert, wobei jeweils zwei hierarchische Parametrisierungen unterschieden werden. Der zweite theoretische Teil dieser Arbeit beschäftigt sich mit der intrinsischen Vermeidung aller geometrischen Locking-Effekte, vor allem aber von Membranlocking. Es wird ein neuartiges, reparametrisiertes gemischtes Prinzip vorgestellt, in dem ausschließlich Verschiebungsgrößen als Primärvariablen auftreten. Diese Reparametrisierung führt dazu, dass die für gemischte Methoden notwendige Wahl geeigneter Spannungs- oder Verzerrungsräume entfällt. Die daraus resultierende intrinsische Vermeidung geometrischer Locking-Effekte verspricht ein breites Anwendungsspektrum dieser Methode.

Abstract

In this contribution a class of formulations for beams, plates and shells is presented, which intrinsically avoids locking, independent of the utilized discretization scheme. The key idea is the reparametrization of the kinematic equations to avoid locking on theory level – prior to discretization. Thus, the resulting formulations are locking‐free for any equal‐order interpolation. As demonstrator, we present both mixed and primal concepts for Timoshenko beams in both weak and strong form, as well as their theoretical relationships. Besides a weak form Galerkin‐type solution using B‐Splines, we show the generality of the presented concepts by employing isogeometric collocation based on the corresponding Euler‐Lagrange equations of the boundary value problem. The quality of both stress resultants and displacements is investigated. Although the underlying concept addresses beams, plates and shells, the present contribution illustrates the methodology for the Timoshenko beam.

Abstract

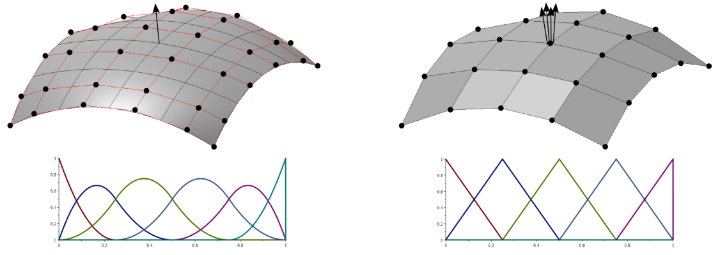
The higher inter-element continuity of the Isogeometric Analysis (IGA) applying NURBS functions for geometry as well as mechanics opens up new possibilities in the analysis of thin-walled structures, i.e. beams, plates and shells. An important advantage is the straightforward implementation of classical theories, which require C1-continuity, e. g. Kirchhoff-Love shell formulations. Based on these "simplest" models shear deformable theories, introducing Timoshenko and Reissner-Mindlin kinematics, are formulated in a hierarchic manner. In contrast to using total rotations the present formulations introduce incremental transverse shear rotations as primary variables. This reparametrization of the kinematic equations can be established in several different fashions, which is addressed in this contribution. All parametrizations have in common, that they lead to shear deformable beam, plate and shell formulations being intrinsically free from transverse shear locking. This is a remarkable feature since the spectrum of different smooth discretization schemes in IGA and other fields of computational shell analysis is continuously growing and the proposed hierarchic shell formulations are locking-free, independent of the underlying discretization.

Abstract

Two novel hierarchic finite element formulations for geometrically nonlinear shell analysis including the effects of transverse shear are presented. Both methods combine a fully nonlinear Kirchhoff-Love shell model with hierarchically added linearized transverse shear components. Thus, large rotations can be taken into account while circumventing the peculiar task of finding a corresponding parametrization of the rotation tensor. The two formulations differ in the way the transverse shear effects are included, either using hierarchic rotations or hierarchic displacements. The underlying assertion is that in most practical applications the transverse shear angles are small even for large deformations. This is confirmed by various numerical experiments. The hierarchic construction results in an additive strain decomposition into parts resulting from membrane and bending deformation and additional contributions from transverse shear. It requires at least C1-continuous shape functions, which can be easily established within the isogeometric context using spline based finite elements. As reported earlier, this concept is intrinsically free from transverse shear locking. In the nonlinear case it dramatically facilitates representation of large rotations in shell analysis.

Abstract

The higher inter-element continuity of the Isogeometric Analysis (IGA) applying NURBS functions for geometry as well as mechanics opens up new possibilities in the analysis of thin-walled structures, i.e. beams, plates and shells. The contribution addresses the straightforward implementation of classical theories requiring C1-continuity, such as the Euler-Bernoulli beam and Kirchhoff-Love shell theory. Based on these “simplest” models shear deformable theories, introducing Timoshenko and Reissner-Mindlin kinematics, are formulated in a hierarchic manner. In contrast to the usual Finite Element concept using total rotations the present model picks up traditional formulations introducing incremental rotations as primary variables. Furthermore an alternative version is discussed with a split of the displacements into bending and transverse shear parts. Both hierarchic concepts can be easily extended to 3D–shell models. The key aspect of this alternative parameterization is the complete a-priori removal of the transverse shear locking and curvature thickness locking (in the case of 3D-shells).

Abstract

A finite element formulation for a geometrically linear, shear deformable (Reissner–Mindlin type) shell theory is presented, which exclusively uses displacement degrees of freedom. The total displacement is subdivided into a part representing the membrane and bending deformation, enriched by two extra “shear displacements”, representing transverse shear deformation. This rotation-free approach is accomplished within the isogeometric concept, using C1-continuous, quadratic NURBS as shape functions. The particular displacement parametrization decouples transverse shear from bending and thus the formulation is free from transverse shear locking by construction, i.e. locking is avoided on the theory level, not by choice of a particular discretization. Compared to the hierarchic formulation proposed earlier within the group of the authors (Echter et al., 2013), the method presented herein avoids artificial oscillations of the transverse shear forces. Up to now, a similar, displacement based method to avoid membrane locking has not been found. Thus, in the present formulation the mixed method from Echter et al. (2013) is used to avoid membrane locking.

Abstract

A hierarchic family of isogeometric shell finite elements based on NURBS shape functions is presented. In contrast to classical shell finite element formulations, inter-element continuity of at least C1 enables a unique and continuous representation of the surface normal within one NURBS patch. This does not only facilitate formulation of Kirchhoff-Love type shell models, for which the standard Galerkin weak form has a variational index of 2, but it also offers significant advantages for shear deformable (Reissner-Mindlin type) shells and higher order shell models. For a 5-parameter shell formulation with Reissner-Mindlin kinematics a hierarchic difference vector which accounts for shear deformations is superimposed onto the rotated Kirchhoff-Love type director of the deformed configuration. This split into bending and shear deformations in the shell kinematics results in an element formulation which is free from transverse shear locking without the need to apply further remedies like reduced integration, assumed natural strains or mixed finite element formulations. The third member of the hierarchy is a 7-parameter model including thickness change and allowing for application of unmodified three-dimensional constitutive laws. The phenomenon of curvature thickness locking, coming along with this kinematic extension, again is automatically avoided by the hierarchic difference vector concept without any further treatment. Membrane locking and in-plane shear locking are removed by two different approaches: firstly elimination via the Discrete Strain Gap (DSG) method and secondly removal of parasitic membrane strains using a hybrid-mixed method based on the Hellinger-Reissner variational principle. The hierarchic kinematic structure of the three different shell formulations allows a straightforward combination of these elements within one mesh and is thus the ideal basis for a model adaptive approach.

Abstract

The present work addresses the development of a hierarchic family of shell models and accompanying discretization schemes with NURBS (Non-Uniform Rational B-Splines) functions that are suitable for the analysis of both thick and thin shell structures. The hierarchy in the shell mechanics is based on a minimalistic 3-parameter formulation, which mechanically corresponds to the shear-rigid Kirchhoff-Love shell model. It is particularly suitable for modeling thin structures with predominantly membrane and bending action. Transverse shear effects and extensibility of the shell in thickness direction are not accounted for. The assumed linear kinematics of the thin shell can be described with three independent parameters, which correspond to the mid-surface displacement components of a material point. No rotations are defined as additional degrees of freedom such that the formulation is rotation-free. Linear-elastic and isotropic material properties are assumed. For asymptotic correctness of the model the constitutive law is modified by implementing the stress condition sigma_33 = 0 to eliminate epsilon_33 via static condensation. Additionally, Love’s first approximation, neglecting contributions with regard to curvature in thickness direction of the shell is not considered. Consequently, membrane and bending action are coupled due to nonzero off-diagonal blocks in the constitutive matrix. No pre-integration of the material law is performed. The static and kinematic variables of the shell equations are therefore stresses and strains. With increasing thickness of the structure, transverse shear effects become more pronounced, thus significantly contributing to the total strain energy of the system. For the Reissner-Mindlin shell model developed in this work, the Kirchhoff-Love assumption is relaxed by introducing additional parameters, which do not depend on the gradient of the mid-surface displacement field and thus allow for extra transverse shear effects. These parameters are introduced via a hierarchic difference vector. The inextensibility of the director in the deformed configuration reduces the number of additionally required parameters to two. In the geometrically linear case, the inextensibility constraint is con- structed by expressing the components of difference vector with respect to the in-plane base vectors of the reference shell mid-surface. In order to account for changes in thickness direction additionally, a 7-parameter shell formulation is derived, which represents an extension of the Reissner-Mindlin-type model with five parameters. The 7-parameter shell model incorporates extensibility of the director in thickness direction and enables the application of three-dimensional constitutive laws without the need of modifications. The main innovation of this thesis is based on the hierarchic parametrization of the family of 3-, 5- and 7-parameter shell formulations, which results in significant benefits both with regard to model-adaptivity and finite element technology. The common approach in FEA consists of adding a difference vector on the director of the undeformed configuration. As a result, continuity requirements on the applied function spaces are reduced. It represents the first Reissner-Mindlin-type shell formulation to be used in this work. Equal-order interpolation of both the mid-surface displacement field and the difference vector, however, results in transverse shear locking which is verified in several numerical plate bending experiments. Alternatively, a hierarchic parametrization is derived for the Reissner-Mindlin model that imposes a shear vector on the rotated director of the 3-parameter Kirchhoff-Love formulation. The procedure of adding the extra parameters is defined so that the kinematic equations of the basic Kirchhoff-Love model are gradually enhanced to obtain the shear flexible 5-parameter model, without the need of a complete new description of the shell kinematics. Although exactly representing the same shell model, with regard to finite element discretization, the hierarchic parametrization of the current director avoids transverse shear locking already in a pure displacement formulation. The ansatz to split the total deformation of the Reissner-Mindlin shell model into independent components related to bending and shear in principal follows Basar and Krätzig (1985) and was used in a similar way for shear-deformable subdivision-based shell finite elements in Long et al. (2012). In Basar and Krätzig (1985) the authors applied the decomposition of the rotation of the shell director into the contribution of the deformed shell normal (Kirchhoff-Love) and rotations related to shear. This allows to derive Kirchhoff-Love theories from shear deformation formulations by simply removing the transverse shear contribution. For FEA, this approach, moreover, offers the significant advantage of an independent parametrization of the transverse shear and consequently avoids incompatibilities of the discrete function spaces in the corresponding kinematic equations. For a decreasing shell thickness the solution asymptotically converges to the Kirchhoff-Love solution, whereas removal of the shear vector directly recovers the 3-parameter Kirchhoff-Love model. The hierarchic 7-parameter shell formulation represents an extension of the hierarchic 5-parameter Reissner-Mindlin shell model. In order to account for extensibility of the director and linear transverse normal strains, the kinematics of the Reissner-Mindlin formulation is enriched with a 6th and 7th displacement parameter, which ultimately yields linear and quadratic displacement contributions across the thickness. By switching off the linear and quadratic displacement contributions in thickness direction, the kinematics of the hierarchic 5-parameter Reissner-Mindlin model can be obtained, whereas further elimination of the difference vector yields the kinematic equations of the 3-parameter Kirchhoff-Love shell. This consequently allows for a straightforward combination of these three element types within one mesh and thus serves as an ideal basis for a model adaptive approach. Numerical experiments in this thesis demonstrate that besides transverse shear locking also curvature thickness locking is by default avoided in pure displacement-based 7-parameter shell finite elements due to the concept of a hierarchic parametrization. The non-hierarchic 7-parameter shell elements with pure displacement formulation and difference vector to be imposed on the director of the undeformed configuration are sensitive to both transverse shear and curvature thickness locking on the contrary. The continuity requirements on the displacement functions for the proposed hierarchic 5- and 7-parameter shell models are identical to those of the 3-parameter Kirchhoff-Love formulation, i.e. C1. The demand for shape functions with square integrable partial derivatives of order two, however, can be naturally satisfied with the higher-continuity NURBS discretizations used in this work. NURBS which represent the standard functions of computer-aided engineering design are applied as shape functions in an isoparametric finite element concept following the isogeometric method of Hughes and coworkers (Hughes et al. (2005), Cottrell et al. (2009)). Their higher continuity property additionally enables a pointwise exact definition of the shell director in the entire patch domain. The effect of higher-order and higher-continuity NURBS discretizations on the accuracy of the discrete solution functions is investigated and analyzed in several numerical experiments. Computational results of higher-continuity NURBS are provided to demonstrate the superior accuracy compared to C0-continuous discretizations. Additionally, analysis of the most prominent locking effects that may show up for the displacement-based isogeometric shell finite elements reveals that the in-plane part of all shell elements developed in this thesis is, in general, considerably prone to locking. Therefore, two new strategies to remove geometric locking effects from higher-order and higher-continuity NURBS discretizations were developed and applied to the membrane part of the shell elements to cure locking: First, the DSG approach of Bletzinger et al. (2000) was successfully transferred to higher-order and higher-continuity NURBS discretizations in order to remove membrane and in-plane shear locking. Second, a mixed displacement-stress formulation which is based on a two-field Hellinger-Reissner variational principle with independent displacement and stress fields is applied to the in-plane strain components of the shell elements. The modified isogeometric Kirchhoff-Love and hierarchic 5- and 7-parameter shell formulations are completely free from geometric locking. Higher-continuity NURBS shape functions to be used for the discretization of the displacement fields in general result in continuous strain and stress distributions which in the case of the NURBS-DSG method may result in a coupling of degrees of freedom that compromises computational efficiency. In several benchmark problems the performance of the newly developed hierarchic shell elements is proven. For the displacement-based element formulations the numerical results conform well with the results from literature like for example from Kiendl et al. (2009). Modification of the membrane part with the mixed displacement-stress ansatz successfully removes locking and leads to significantly faster convergence of the investigated results to the reference solutions. For multipatch analysis, the penalty-type bending strip method of Kiendl et al. (2010) is used to connect NURBS surface patches with slope continuity in a weak sense. Appropriate stiffness parameters for the bending strips are defined according to Kiendl (2011). The isogeometric analysis of highly-curved respectively thick shell structures reveals significant differences in the system response for the three different shell models (3-, 5- and 7-parameter). Simultaneously, a fast diminution of the influence of both transverse shear and higher-order mechanical effects on the investigated displacement results can be observed. For model adaptivity, analysis of the same problem setup is performed with hierarchic 5-parameter Reissner-Mindlin shell elements by systematically deacti- vating those degrees of freedom related to the shear vector. The computational results obtained, perfectly match the 3-parameter Kirchhoff-Love solution.

Abstract

The strategy of using finite elements with NURBS shape functions for of both geometry and displacements (“isogeometric approach”) is investigated from the point of view of finite element technology. Convergence rates are compared to those of classical finite element approaches utilizing standard Lagrange shape functions. Moreover, typical locking phenomena are examined. It is found that higher order inter-element continuity within the NURBS approach results in identical convergence rates but smaller absolute errors compared to C0-continuous approaches. However, NURBS finite elements suffer from the same locking problems as finite elements using Lagrange shape functions. The discrete shear gap (DSG) method, a general framework for formulation of locking-free elements, is applied to develop a new class of NURBS finite elements. The resulting NURBS DSG elements are absolutely free from locking and preserve the property of improved accuracy compared with standard locking-free finite elements. The method is exemplified for the Timoshenko beam model, but may be applied to more general cases.