Vortrag am KIT von Alexander Müller: "Optimization on Manifolds for the Advanced Discretization of Director Fields"

Alexander Müller vom Institut für Baustatik und Baudynamik ist zu Gast am Karlsruher Institut für Technologie und hält einen Vortrag im Seminar des Instituts für Mechanik zum Thema

"Optimization on Manifolds for the Advanced Discretization of Director Fields"

Zur Person: Alexander Müller

Zum Vortrag:

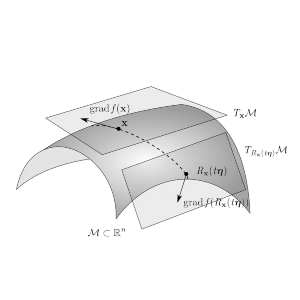
Optimization problems often incorporate constraints, which can be addressed using methods such as the penalty method or introducing Lagrange multipliers. However, these approaches often introduce unsatisfactory features to the optimization process, such as dependence on a penalty parameter or the transformation of a minimization problem into a saddle-point problem. Fortunately, these constraints can sometimes be interpreted as restrictions on the design space. The formulations realize this by transforming the problem from "constrained optimization on an unconstrained space" to "unconstrained optimization on a constrained space," preserving the structure of the problem and allowing dimensional reduction of the design space.

This is particularly true for so-called director fields, which typically arise in geometrically non-linear structural models, such as the Reissner-Mindlin shell model or three-dimensional beam models. They also emerge in material models of Cosserat-type and in micromagnetic simulations. The pertinent constraint is maintaining the unit length of the director during deformation.

In the specific case of directors with unit length, the manifold is the unit sphere. For a director triad of orthonormal vectors, this manifold is the three-dimensional special orthogonal group. The corresponding transformation is the special orthogonal group. This transformation to an unconstrained optimization problem on a manifold requires the careful generalization of seemingly innocent concepts. For example, it involves generalizing the incremental update of design variables. If these variables reside on a manifold (instead of a linear vector space), the simple addition of the incremental update and the design variable is not well-defined, and alternative concepts are needed, such as addition in tangent spaces and exponential mapping. These properties are demonstrated in the context of micromagnetics and Reissner-Mindlin shells through a set of numerical examples.

Magnetisierung in einem zylindrischen magnetischen nanodot mit Wirbel im Zentrum
[Bild: Alexander Müller]

Optimierung auf Mannigfaltigkeiten: Retraction und andere riemannsche Größen
[Bild: Alexander Müller]